Een tweeduizend jaar oude methode om priemgetallen te vinden heeft een upgrade gekregen. Daardoor heeft een computer straks minder geheugen nodig om grote getallen te doorzoeken.
Priemgetallen zijn getallen die je alleen kunt delen door 1 en het getal zelf. Ze vormen de bouwstenen van alle andere getallen. Door priemgetallen met elkaar te vermenigvuldigen, kun je namelijk elk ander getal creëren.
In 240 voor Christus ontwikkelde de oud-Griekse wiskundige Eratosthenes een methode om priemgetallen op te sporen. Met de ‘zeef van Eratosthenes’ kun je elk priemgetal vinden dat kleiner is dan een bepaald getal. Dat doe je door alle veelvouden van priemgetallen weg te zeven.
Neem bijvoorbeeld de getallen 1 tot en met 100. Je begint dan met het weghalen van alle veelvouden van 2, het eerste priemgetal. Je zeeft dus 2, 4, 6, 8 enzovoort weg. Daarna begin je opnieuw bij het kleinste overgebleven getal: dan haal je alle veelvouden van 3 weg. Vervolgens moet je eerst de veelvouden van 5 en daarna die van 7 zeven, en zo ga je verder tot je niet meer verder kunt. Elk getal waarbij je het proces begint – en dat dus niet al is weggehaald – is een priemgetal.
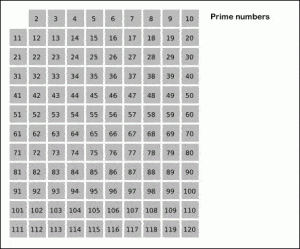
Deze zeef werkt goed om kleine priemgetallen te vinden. Voor heel grote exemplaren is die echter onbruikbaar. Dan kost de methode een computer erg veel tijd en geheugen.
Rijen van tien
In de jaren zestig, toen computers nog veel minder geheugen hadden dan nu, verbeterden wiskundigen de zeef. Daardoor had een computer om alle priemgetallen kleiner dan een bepaald getal N te vinden slechts √N eenheden aan opslagruimte nodig. Een algoritme kon dan bijvoorbeeld alle priemgetallen onder de honderd vinden door getallen in rijen van tien op te slaan en te verwerken.
Maar voor veel grotere waarden van N is ook dat niet langer praktisch. ‘Je kunt niet een miljard getallen analyseren met slechts tien opslageenheden per tijdseenheid. Het algoritme wordt dan heel inefficiënt’, zegt Harald Helfgott van de universiteit van Göttingen in Duitsland.
Breukbenadering
Helfgott heeft de methode nu een upgrade gegeven. Daarbij gebruikt hij de ‘diofantische benadering’: een methode waarbij je reële getallen – elk punt op de getallenlijn, inclusief decimalen – benadert met rationale getallen. Dat zijn getallen die je kunt uitdrukken als een breuk van twee gehele getallen. Pi is bijvoorbeeld een reëel getal dat je kunt benaderen met de breuk 355/113.
Dankzij de diofantische benadering kan Helfgott een hele serie getallen tegelijk doorzeven, wat het proces efficiënter maakt. Daardoor heeft het algoritme minder computergeheugen nodig om alle priemgetallen kleiner dan een bepaald getal N te vinden – ongeveer N1/3(log N)2/3 opslageenheden. Op die manier kun je een miljard getallen doorzeven met ongeveer 7500 geheugeneenheden, tegenover 32.000 met de huidige methode.
Echte programmeurs
Helfgotts benadering kan ook van pas komen om heel grote getallen te ontbinden in priemfactoren. Daarbij breek je ze af tot priemgetal-bouwblokjes.
Momenteel zijn de voordelen van de nieuwe methode nog puur theoretisch. Helfgott heeft namelijk geen algoritme gemaakt dat je op een computer kunt draaien. ‘Hoeveel verschil dit in de praktijk maakt, zullen we pas weten wanneer echte programmeurs het programma verwezenlijken en optimaliseren’, zegt hij.
Het resultaat is gepubliceerd in vakblad Mathematics of Computation.
