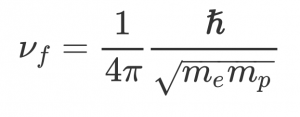Hoe vloeiend kan een vloeistof zijn? Een verrassend simpele formule geeft het antwoord.
Natuurkundige Kostya Trachenko van de Queen Mary Universiteit in Londen en Vadim Brazhkin van de Russische Academie der Wetenschappen hebben een formule ontwikkeld die laat zien hoe vloeiend een vloeistof kan zijn. De formule, gepubliceerd in Science Advances, is gestoeld op enkele fundamentele natuurkundige constanten. Daardoor heeft die allerlei toepassingen – van de ontwikkeling van schoonmaakproducten tot sterrenkundig onderzoek.
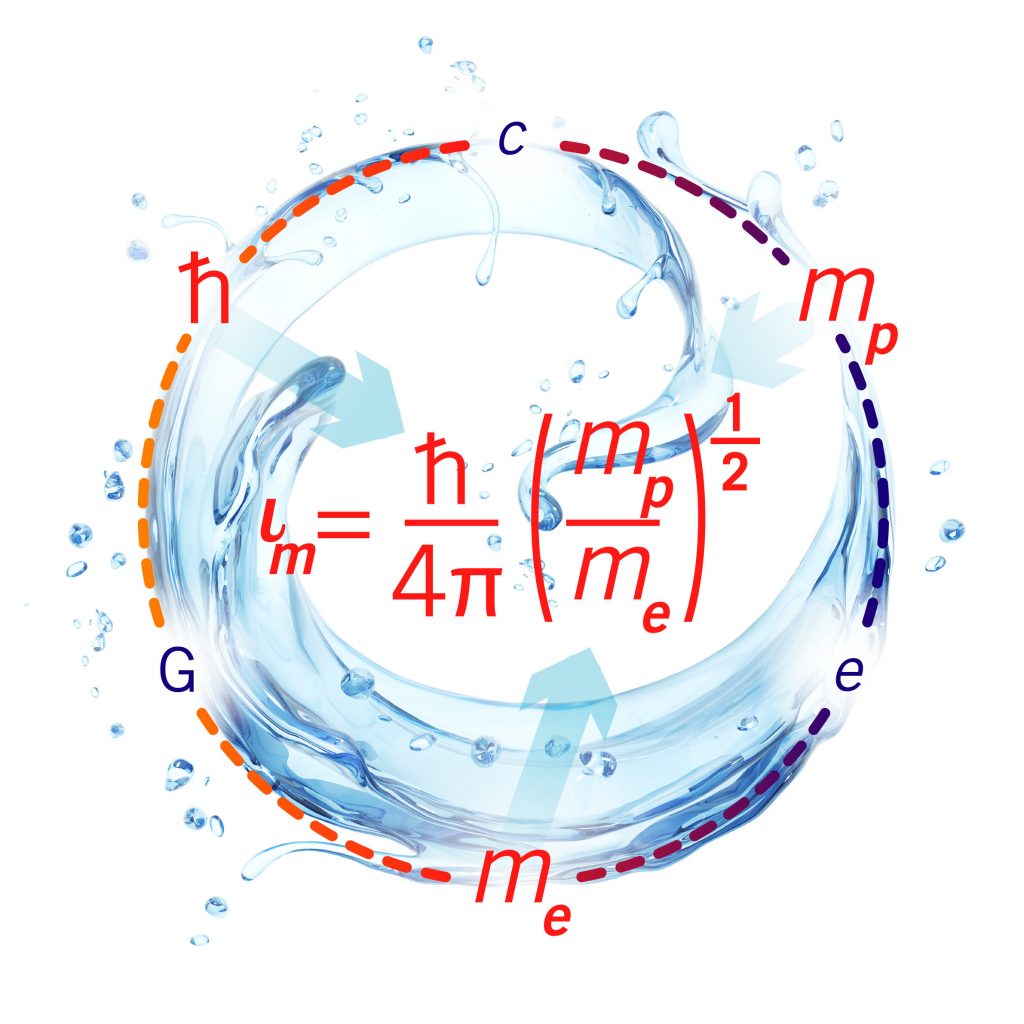
Hoe vloeiend een vloeistof is, geven natuurkundigen aan met de zogeheten viscositeit. Hoe hoger de viscositeit, hoe stroperiger de vloeistof. Hoe lager de viscositeit, hoe vloeiender.
De viscositeit hangt onder andere af van de temperatuur van de vloeistof en de druk die erop heerst. Wanneer je bijvoorbeeld water opwarmt, wordt het steeds vloeiender. Maar dat houdt een keer op: onder normale druk verdampt water bij 100 graden Celsius. Het is dan geen vloeistof meer, maar een gas.
Tijdens die faseovergang gebeuren op moleculair niveau allerlei gekke dingen, zoals het ontstaan van bellen in het water. Die verschijnselen verhogen de viscositeit. Daardoor is kokend water weliswaar behoorlijk vloeiend, maar bereikt het niet de minimale viscositeit die het in theorie kan hebben.
Simpel en universeel
Doordat de viscositeit van een vloeistof afhangt van allerlei interne en externe factoren, dachten wetenschappers dat het onmogelijk was om zo’n theoretisch minimum te bepalen. Trachenko en Brazhkin bewezen het tegendeel: ze stelden een formule op voor de minimale viscositeit van een vloeistof. En voor een natuurkundige formule blijkt die verrassend simpel: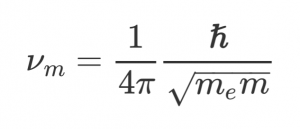
Hierbij is νm de minimale kinematische viscositeit, oftewel de viscositeit afgezet tegen de dichtheid van de vloeistof. m is de massa van één vloeistofmolecuul, me is de massa van een elektron en de doorgestreepte h is de constante van Planck gedeeld door 2π. Die laatste twee factoren zijn fundamentele natuurconstanten: getallen die altijd en overal hetzelfde zijn. Hoe vloeiend een vloeistof kan zijn, hangt dus eigenlijk alleen af van de dichtheid van die vloeistof en de massa van één molecuul.
‘Dit resultaat is verbijsterend’, zegt Trachenko. ‘Viscositeit is een complexe eigenschap die sterk afhangt van het type vloeistof en de omstandigheden. Toch laat ons onderzoek zien dat de minimale viscositeit van alle vloeistoffen simpel en universeel is.’
Wanneer je bijvoorbeeld de minimale kinematische viscositeit van water wilt uitrekenen, vul je voor m simpelweg de massa van één H2O-molecuul in. De minimale viscositeit van waterstof is al helemaal eenvoudig uit te rekenen. Waterstof bestaat uit een proton en een elektron. Aangezien een proton vele malen zwaarder is dan een elektron, kun je voor m alleen de protonmassa invullen. De formule voor de minimale kinematische viscositeit van waterstof bestaat daarmee uit louter fundamentele natuurconstanten:
Kernreacties in sterren
Om de formule er nog wat fundamenteler uit te laten zien, introduceerden de natuurkundigen het begrip ‘elementaire viscositeit’. Dat is de viscositeit van een vloeistof vermenigvuldigd met het volume dat één molecuul inneemt, oftewel de minimale kinematische viscositeit vermenigvuldigd met de massa van één molecuul. De elementaire viscositeit wordt gegeven door:
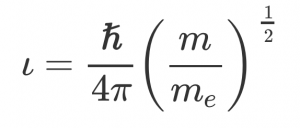Doordat de molecuulmassa hier boven de deelstreep staat, kun je de minimale waarde vinden door de massa van het lichtste molecuul, atomair waterstof, in te vullen:
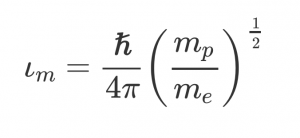Deze schrijfwijze van de formule is de favoriet van Trachenko en Brazhkin. Je ziet hier namelijk dat de minimale elementaire viscositeit afhangt van de verhouding tussen de protonmassa en de elektronmassa. Deze verhouding zie je ook op heel andere gebieden terug, bijvoorbeeld in formules die de kernreacties beschrijven die binnenin sterren plaatsvinden. Deze reacties bepalen onder andere of een ster uiteindelijk instort tot een neutronenster of een zwart gat.
‘Er zijn aanwijzingen dat de fundamentele ondergrens van de viscositeit van vloeistoffen verband houdt met compleet andere onderzoeksvelden in de natuurkunde’, zegt Brazhkin. ‘Het onderzoeken en waarderen van dergelijke verbanden maakt wetenschap zo spannend.’
Superkritisch
De natuurkundigen kwamen tot de formules door eerst te kijken naar experimentele data over de viscositeit van superkritische vloeistoffen. Dat zijn vloeistoffen die onder een hoge temperatuur en druk staan. In dat geval veranderen ze niet in een gas, hoezeer je ze ook opwarmt.
Daardoor kun je de viscositeit ervan bestuderen zonder dat die beïnvloed wordt door de gekke verschijnselen die bij de faseovergang optreden. Uit de data bleek dat superkritische vloeistoffen weliswaar altijd vloeibaar blijven als je ze opwarmt, maar niet alsmaar vloeiender worden. Bij een bepaalde temperatuur bereiken ze een minimum. Als je ze nog verder opwarmt, worden ze weer stroperiger.
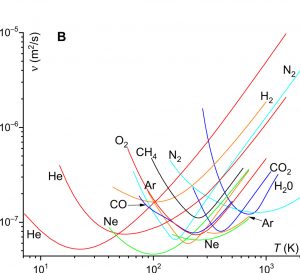
Door de minimale viscositeit van verschillende superkritische vloeistoffen onder verschillende druk te vergelijken, konden de natuurkundigen de theoretische minimale waarde vaststellen. Vervolgens bekeken ze experimentele data over de viscositeit van vloeistoffen bij normale temperatuur en druk. Die vloeistoffen bleken bij opwarming op de voorspelde minimale viscositeit af te koersen. Ze bereiken die alleen nooit, doordat de viscositeit tijdens de faseovergang plots omhoogschiet.
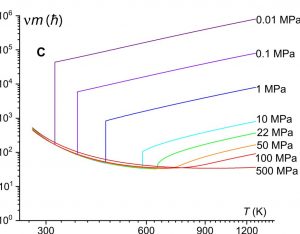
Superkritische vloeistoffen worden sinds kort gebruikt om bepaalde afvalproducten te laten oplossen. Hoe vloeiender zo’n vloeistof, hoe beter die werkt. Dankzij de formules weten onderzoekers nu wat de minimale viscositeit is die ze kunnen nastreven. Ook weten ze wanneer het geen zin meer heeft om een nog vloeiender product te willen ontwikkelen, omdat de fundamentele natuurwetten dat vanaf een bepaald punt verbieden.
