Velen van ons hoopten op sneeuw, maar het lijkt erop dat we genoegen moeten nemen met niet-witte kerstdagen. Om toch een beetje weg te kunnen dromen bij sneeuwvlokjes, bieden we bovenstaande video aan. Professor Adrian Bejan van de Amerikaanse universiteit Duke legt hierin uit hoe sneeuwvlokjes ontstaan. Hij onthult daarbij een bekend misverstand: sneeuwvlokjes zijn niet uniek.
Altijd zes
Althans, tot op zekere hoogte. Wanneer een groeiend sneeuwblokje door de atmosfeer beweegt, ervaart hij namelijk kleine veranderingen in temperatuur en vochtigheid. Die subtiele verschillen bepalen zijn uiteindelijke vorm. Waar professor Bejan wel gelijk in heeft, is dat elk sneeuwvlokje zes zijden zal tellen.
Maar waarom? Waarom heeft een vlokje niet acht kanten (zoals Google dacht toen ze in 2010 hun kerstdoodle ontwierpen)? Om dat te begrijpen moeten we flink inzoomen: de zes zijden zijn te verklaren door de vorm van watermoleculen.
V-vorm
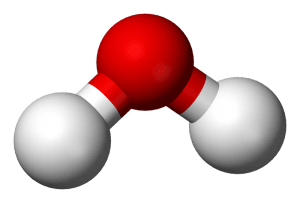Een watermolecuul is geen bolletje, maar heeft een V-vorm. In de punt van de V zit een zuurstofatoom (O), waarop twee waterstofatomen (H) zijn geprikt. Wanneer een dwarrelend sneeuwvlokje een waterdruppel tegenkomt, zullen een aantal van deze V-vormige watermoleculen aan de V-vormige watermoleculen van het vlokje blijven plakken. Maar welke zijde plakt waar?
Het O-atoom in het watermolecuul trekt sterk aan de elektronen van de twee H-atomen. Daardoor is de kant van de H-atomen net wat positief geladen. De punt van de V is juist wat negatief. Zodra een watermolecuul tegen het vlokje valt, zullen de negatieve kanten van het vlokje de positieve kanten van de zwervende druppel aantrekken. Het resultaat: een driedimensionaal patroon met een zeszijdige symmetrie:
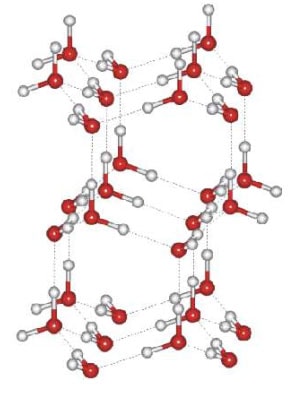Het gehele vlokje volgt simpelweg de regels van deze structuur. En daarmee is elk vlokje wat minder uniek en eigenwijs dan veel mensen denken. Wie weet kan die kennis je nog van pas komen tijdens discussies aan de kersttafel.