Vandaag is het Fibonacci-dag! De rij van Fibonacci is innig verbonden met het bijzondere getal φ, beter bekend als de gulden snede. Hier lees je waarom φ wordt gezien als het meest irrationale getal van allemaal.
Leonardo van Pisa, bijgenaamd Fibonacci, is een wiskundige uit de middeleeuwen. Hij is vooral bekend van de rij van Fibonacci. Dat is een getallenrij die begint met nul en één, waarbij je elk volgend getal krijgt door de vorige twee op te tellen:
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89…
Aan de eerste getallen zie je waarom deze dag is uitgeroepen tot jaarlijkse Fibonacci-dag: 23 november schrijf je op z’n Amerikaans als 11/23.
Eindeloze decimalen
De rij van Fibonacci houdt verband met een van de beroemdste getallen die er bestaan: de gulden snede. Dit getal krijg je wanneer je een lijnstuk zodanig in tweeën deelt, dat de verhouding tussen het grote en kleine deel hetzelfde is als de verhouding tussen het hele lijnstuk en het grote deel – iets wat je beter met een plaatje kunt uitdrukken:
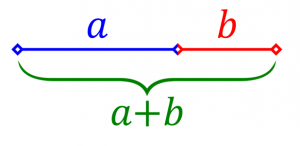
De verhouding tussen de lijnstukken is hier gelijk aan de gulden snede:
Door deze formule te herschrijven, kun je de waarde van φ uitrekenen:
Dit getal bevat een eindeloze rij decimalen, zonder dat die zichzelf op een gegeven moment herhalen. Dat betekent dat je de gulden snede niet als gewone breuk kunt schrijven – dus niet als een deling tussen twee gehele getallen. Daarmee is φ een irrationaal getal.
Droste-breuk
Op zichzelf is dat niet zo bijzonder. Er zijn oneindig veel meer irrationale dan rationale getallen. Andere bekende voorbeelden zijn π (3,14159…), het exponentiële getal e (2,71828…) en de wortel van twee (1,41421…).
Wat wel bijzonder is: volgens wiskundigen is de gulden snede het meest irrationale getal dat er bestaat. Dat komt doordat je φ kunt schrijven als een zogeheten kettingbreuk. Dat is een breuk waarbij het Droste-effect optreedt: een breuk in een breuk in een breuk in een breuk…
Bij de gulden snede is de kettingbreuk op deze manier opgebouwd:
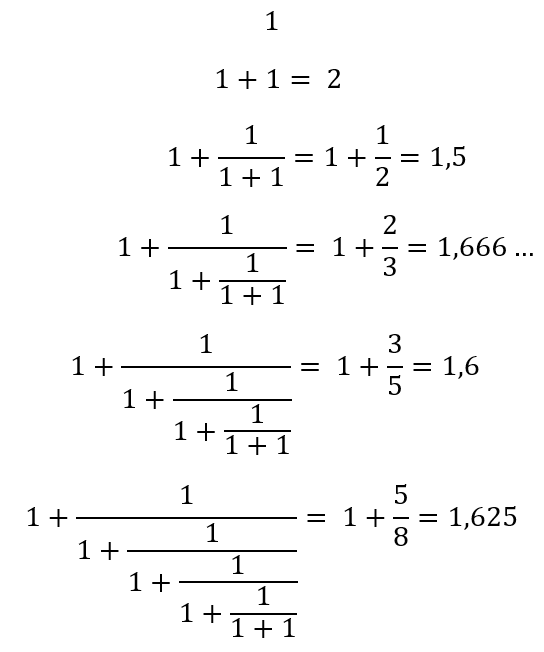
Je ziet dat je zo steeds dichter bij de echte waarde van φ komt. Maar je komt er nooit helemaal; de kettingbreuk gaat eindeloos door. Dat maakt de gulden snede irrationaal.
Bovendien bevat de breuk alleen maar enen. Daarmee is het een eindeloze kettingbreuk in zijn meest zuivere vorm. En daarom beschouwen wiskundigen de gulden snede als het meest irrationale getal.
Doen de meest rechter breuken in de sommen hierboven je trouwens ergens aan denken? Inderdaad: daar zie je het verband met de rij van Fibonacci. Je kunt de gulden snede ook benaderen door twee opeenvolgende termen uit die rij door elkaar te delen. Het liefst zo hoog mogelijk: 89/55 is bijvoorbeeld 1,618181… Fijne Fibonacci-dag!
